これ以上何を失えば 心は許されるの
코레이죠- 나니오 우시나에바 코코로와 유루사레루노
이 이상 뭘 잃어야 마음이 허락되나요

どれ程の痛みならば もういちど君に會える
도레호도노 이타미나라바 모- 이치도 키미니 아에루
어느 정도의 아픔이라면 다시 한 번 그대를 만날 수 있나요

One more time 季節よ うつろわないで
One more time 키세츠요 우츠로와나이데
One more time 계절이여 변하지 말아요

One more time ふざけあった 時間よ
One more time 후자케앗타 지캉요
One more time 서로 장난쳤던 시간이여

くいちがう時はいつも 僕が先に折れたね
쿠이치가우 토키와 이츠모 보쿠가 사키니 오레타네
서로 의견이 맞지 않을 때는 언제나 내가 먼저 양보했었죠

わがままな性格が なおさら愛しくさせた
와가마마나 세-카쿠가 나오사라 이토-시쿠 사세타
네 멋대로인 그대의 성격이 더욱 사랑스럽게 했죠

One more chance 記憶に足を取られて
One more chance 키오쿠니 아시오 토라레테
One more chance 기억에 발이 묶여서

One more chance 次の場所を選べない
One more chance 츠기노 바쇼-오 에라베나이
One more chance 다음에 갈 장소를 고를 수 없어요

いつでも搜しているよ どっかに君の姿を
이츠데모 사가시테-루요 독카니 키미노 스가타오
언제나 찾고 있어요 어딘가에서 그대의 모습을

向いのホ-ム 路地裏の窓
무카이노 호-무 로지우라노 마도
반대편의 플랫폼 뒷골목의 창문

こんなとこにいるはずもないのに
콘나 토코니 이루하즈모 나이노니
이런 곳에 있을리가 없는데도

願いがもしもかなうなら 今すぐ君のもとへ
네가이가 모시모 카나우나라 이마 스구 키미노 모토에
소원이 만약에 이뤄진다면 지금 바로 그대가 있는 곳으로

できないことは もう何もない
데키나이 코토와 모- 나니모나이
불가능한 건 이제 아무것도 없어요

すべてかけて抱きしめてみせるよ
스베테 카케테 다키시메테 미세루요
모든 걸 걸고 안아 보일게요

寂しさ紛らすだけなら 誰でもいいはずなのに
사비시사 마기라스 다케나라 다레데모 이이하즈 나노니
외로움을 달래기 위한 것 뿐이라면 다른 아무나 좋았을 텐데

星が落ちそうな夜だから 自分をいつわれない
호시가 오치소-나 요루다카라 지붕오 이츠와레나이
별이 떨어질 것 같은 밤이기에 나 자신을 속일 수 없어요

One more time 季節よ うつろわないで
One more time 키세츠요 우츠로와나이데
One more time 계절이여 변하지 말아요

One more time ふざけあった 時間よ
One more time 후자케앗타 지캉요
One more time 서로 장난쳤던 시간이여

いつでも搜しているよ どっかに君の姿を
이츠데모 사가시테-루요 독카니 키미노 스가타오
언제나 찾고 있어요 어딘가에서 그대의 모습을

交差点でも 夢の中でも
코-사텐데모 유메노 나카데모
교차로에서도 꿈 속에서도

こんなとこにいるはずもないのに
콘나 토코니 이루하즈모 나이노니
이런 곳에 있을리가 없는데도

奇跡がもしも起こるなら 今すぐ君に見せたい
키세키가 모시모 오코루나라 이마스구 키미니 미세타이
기적이 만약에 일어난다면 지금 바로 그대에게 보여주고 싶어요

新しい朝 これからの僕
아타라시- 아사 코레카라노 보쿠
새로운 아침을 앞으로의 내 모습을

言えなかった「好き」という言葉も
이에나캇타「스키」토유-코토바모
말하지 못했던 「좋아한다」는 말도

夏の想い出がまわる Uh...

나츠노 오모이데가 마와루 Uh...
여름의 추억이 머릿속을 맴돌아요 Uh...

ふいに消えた鼓動
후이니 키에타 코도-
갑자기 사라진 고동

いつでも搜しているよ どっかに君の姿を
이츠데모 사가시테-루요 독카니 키미노 스가타오
언제나 찾고 있어요 어딘가에서 그대의 모습을

明け方の街 櫻木町で
아케가타노 마치 사쿠라기쵸-데
새벽녘의 거리 사쿠라기쵸에서

こんなとこに來るはずもないのに
콘나 토코니 쿠루하즈모 나이노니
이런 곳에 올리가 없는데도

願いがもしもかなうなら 今すぐ君のもとへ
네가이가 모시모 카나우나라 이마스구 키미노 모토에
소원이 만약 이루어진다면 지금 바로 그대가 있는 곳으로

できないことは もう何もない
데키나이 코토와 모- 나니모나이
불가능한 건 이제 아무것도 없어요

すべてかけて抱きしめてみせるよ
스베테 카케테 다키시메테 미세루요
모든 걸 걸고 안아 보일게요

いつでも搜しているよ どっかに君の破片を
이츠데모 사가시테-루요 독카니 키미노 카케라오
언제나 찾고 있어요 어딘가에서 그대의 흔적을

旅先の店 新聞の隅
타비사키노 미세 심분노 스미
여행간 곳의 가게에서 신문 구석에서

こんなとこにあるはずもないのに
콘나 토코니 아루하즈모 나이노니
이런 곳에 있을리가 없는데도

奇跡がもしも起こるなら 今すぐ君に見せたい
키세키가 모시모 오코루나라 이마스구 키미니 미세타이
기적이 만약에 일어난다면 지금 바로 그대에게 보여주고 싶어요

新しい朝 これからの僕
아타라시- 아사 코레카라노 보쿠
새로운 아침을 앞으로의 내 모습을

言えなかった「好き」という言葉も
이에나캇타「스키」토유-코토바모
말하지 못했던 「좋아한다」는 말도

いつでも搜してしまう どっかに君の笑顔を
이츠데모 사가시테 시마우 독카니 키미노 에가오오
언제나 찾게 되요 어딘가에서 그대의 웃는 얼굴을

急行待ちの 踏切あたり
큐-코- 마치노 후미키리 아타리
급행을 기다리는 건널목 부근에서

こんなとこにいるはずもないのに
콘나 토코니 이루하즈모 나이노니
이런 곳에 있을리가 없는데도

命が繰り返すならば 何度も君のもとへ
이노치가 쿠리카에스나라바 난도모 키미노 모토에
생명이 반복된다면 몇 번이라도 그대가 있는 곳으로

欲しいものなど もう何もない
호시- 모노나도 모- 나니모 나이
필요한 건 더이상 없어요

君のほかに大切なものなど
키미노 호카니 타이세츠나 모노 나도
그대 외에 소중한 것 따위 없어요

Goal programming is a branch of multiobjective optimization, which in turn is a branch of multi-criteria decision analysis (MCDA), also known as multiple-criteria decision making (MCDM). This is an optimization programme. It can be thought of as an extension or generalisation of linear programming to handle multiple, normally conflicting objective measures. Each of these measures is given a goal or target value to be achieved. Unwanted deviations from this set of target values are then minimised in an achievement function. This can be a vector or a weighted sum dependent on the goal programming variant used. As satisfaction of the target is deemed to satisfy the decision maker(s), an underlying satisficing philosophy is assumed.

History

Goal programming was first used by Charnes, Cooper and Ferguson in 1955,^[1] although the actual name first appear in a 1961 text by Charnes and Cooper.^[2] Seminal works by Lee,^[3] Ignizio,^[4] Ignizio and Cavalier,^[5] and Romero^[6] followed. Schniederjans gives in a bibliography of a large number of pre-1995 articles relating to goal programming,^[7] and Jones and Tamiz give an annotated bibliography of the period 1990-2000.^[8]

The first engineering application of goal programming, due to Ignizio in 1962, was the design and placement of the antennas employed on the second stage of the Saturn V. This was used to launch the Apollo space capsule that landed the first men on the moon.

Variants

The initial goal programming formulations ordered the unwanted deviations into a number of priority levels, with the minimisation of a deviation in a higher priority level being infinitely more important than any deviations in lower priority levels. This is known as lexicographic or pre-emptive goal programming. Ignizio^[4] gives an algorithm showing how a lexicographic goal programme can be solved as a series of linear programmes. Lexicographic goal programming should be used when there exists a clear priority ordering amongst the goals to be achieved.

If the decision maker is more interested in direct comparisons of the objectives then Weighted or non pre-emptive goal programming should be used. In this case all the unwanted deviations are multiplied by weights, reflecting their relative importance, and added together as a single sum to form the achievement function. It is important to recognise that deviations measured in different units cannot be summed directly due to the phenomenon of incommensurability.

Hence each unwanted deviation is multiplied by a normalisation constant to allow direct comparison. Popular choices for normalisation constants are the goal target value of the corresponding objective (hence turning all deviations into percentages) or the range of the corresponding objective (between the best and the worst possible values, hence mapping all deviations onto a zero-one range).^[6] For decision makers more interested in obtaining a balance between the competing objectives, Chebyshev goal programming should be used. Introduced by Flavell in 1976,^[9] this variant seeks to minimise the maximum unwanted deviation, rather than the sum of deviations. This utilises the Chebyshev distance metric, which emphasizes justice and balance rather than ruthless optimisation.

Strengths and weaknesses

A major strength of goal programming is its simplicity and ease of use. This accounts for the large number of goal programming applications in many and diverse fields.^[8] As weighted and Chebyshev goal programmes can be solved by widely available linear programming computer packages, finding a solution tool is not difficult in most cases. Lexicographic goal programmes can be solved as a series of linear programming models, as described by Ignizio and Cavalier.^[4]

Goal programming can hence handle relatively large numbers of variables, constraints and objectives. A debated weakness is the ability of goal programming to produce solutions that are not Pareto efficient. This violates a fundamental concept of decision theory, that is no rational decision maker will knowingly choose a solution that is not Pareto efficient. However, techniques are available ^{[10][6] [11]} to detect when this occurs and project the solution onto the Pareto efficient solution in an appropriate manner.

The setting of appropriate weights in the goal programming model is another area that has caused debate, with some authors ^[12] suggesting the use of the Analytic Hierarchy Process or interactive methods ^[13] for this purpose.

References

Pareto efficiency, or Pareto optimality, is a concept in economics with applications in all areas of the discipline as well as engineering and other social sciences. The term is named after Vilfredo Pareto, an Italian economist who used the concept in his studies of economic efficiency and income distribution. Informally, Pareto efficient situations are those in which it is impossible to make one person better off without necessarily making someone else worse off.

Given a set of alternative allocations of goods or outcomes for a set of individuals, a change from one allocation to another that can make at least one individual better off without making any other individual worse off is called a "Pareto improvement". An allocation is defined as "Pareto efficient" or "Pareto optimal" when no further Pareto improvements can be made. Such an allocation is often called a "strong Pareto optimum (SPO)" by way of setting it apart from mere "weak Pareto optima" as defined below.

Formally, a (strong/weak) Pareto optimum is a maximal element for the partial order relation of Pareto improvement/strict Pareto improvement: it is an allocation such that no other allocation is "better" in the sense of the order relation.

Pareto efficiency does not necessarily result in a socially desirable distribution of resources, as it makes no statement about equality or the overall well-being of a society.^[1][2]

Weak and strong Pareto optimum

A "weak Pareto optimum" (WPO) nominally satisfies the same standard of not being Pareto-inferior to any other allocation, but for the purposes of weak Pareto optimization, an alternative allocation is considered to be a Pareto improvement only if the alternative allocation is strictly preferred by all individuals (i.e., only if all individuals would gain from a transition to the alternative allocation). In other words, when an allocation is WPO there are no possible alternative allocations whose realization would cause every individual to gain.

Weak Pareto-optimality is "weaker" than strong Pareto-optimality in the sense that the conditions for WPO status are "weaker" than those for SPO status: Any allocation that can be considered an SPO will also qualify as a WPO, while the reverse does not hold: a WPO allocation won't necessarily qualify as SPO.

Under any form of Pareto-optimality, for an alternative allocation to be Pareto-superior to an allocation being tested -- and, therefore, for the feasibility of an alternative allocation to serve as proof that the tested allocation is not an optimal one -- the feasibility of the alternative allocation must show that the tested allocation fails to satisfy at least one of the requirements for SPO status. One may apply the same metaphor to describe the set of requirements for WPO status as being "weaker" than the set of requirements for SPO status. (Indeed, because the SPO set entirely encompasses the WPO set, with respect to any property the requirements for SPO status are of strength equal to or greater than the strength of the requirements for WPO status. Therefore, the requirements for WPO status are not merely weaker on balance or weaker according to the odds; rather, one may describe them more specifically and quite fittingly as "Pareto-weaker.")

• Note that when one considers the requirements for an alternative allocation's superiority according to one definition against the requirements for its superiority according to the other, the comparison between the requirements of the respective definitions is the opposite of the comparison between the requirements for optimality: To demonstrate the WPO-inferiority of an allocation being tested, an alternative allocation must falsify at least one of the particular conditions in the WPO subset, rather than merely falsify at least one of either these conditions or the other SPO conditions. Therefore, the requirements for weak Pareto-superiority of an alternative allocation are harder to satisfy -- i.e., "stronger" -- than are the requirements for strong Pareto-superiority of an alternative allocation.)

• It further follows that every SPO is a WPO (but not every WPO is an SPO): Whereas the WPO description applies to any allocation from which every feasible departure results in the NON-IMPROVEMENT of at least one individual, the SPO description applies to only those allocations that meet both the WPO requirement and the more specific ("stronger") requirement that at least one non-improving individual exhibit a specific type of non-improvement, namely DOING WORSE.

• The "strong" and "weak" descriptions of optimality continue to hold true when one construes the terms in the context set by the field of semantics: If one describes an allocation as being a WPO, one makes a "weaker" statement than one would make by describing it as an SPO: If the statements "Allocation X is a WPO" and "Allocation X is a SPO" are both true, then the former statement is less controversial than the latter in that to defend the latter, one must prove everything one must prove to defend the former "and then some." By the same token, however, the former statement is less informative or contentful in that it "says less" about the allocation; that is, the former statement contains, implies, and (when stated) asserts fewer constituent propositions about the allocation.

Pareto efficiency in economics

An economic system that is Pareto inefficient implies that a certain change in allocation of goods (for example) may result in some individuals being made "better off" with no individual being made worse off, and therefore can be made more Pareto efficient through a Pareto improvement. Here 'better off' is often interpreted as "put in a preferred position." It is commonly accepted that outcomes that are not Pareto efficient are to be avoided, and therefore Pareto efficiency is an important criterion for evaluating economic systems and public policies.

If economic allocation in any system (in the real world or in a model) is not Pareto efficient, there is potential for a Pareto improvement — an increase in Pareto efficiency: through reallocation, improvements to at least one participant's well-being can be made without reducing any other participant's well-being.

In the real world ensuring that nobody is disadvantaged by a change aimed at improving economic efficiency may require compensation of one or more parties. For instance, if a change in economic policy dictates that a legally protected monopoly ceases to exist and that market subsequently becomes competitive and more efficient, the monopolist will be made worse off. However, the loss to the monopolist will be more than offset by the gain in efficiency. This means the monopolist can be compensated for its loss while still leaving an efficiency gain to be realized by others in the economy. Thus, the requirement of nobody being made worse off for a gain to others is met.

In real-world practice, the compensation principle often appealed to is hypothetical. That is, for the alleged Pareto improvement (say from public regulation of the monopolist or removal of tariffs) some losers are not (fully) compensated. The change thus results in distribution effects in addition to any Pareto improvement that might have taken place. The theory of hypothetical compensation is part of Kaldor-Hicks efficiency, also called Potential Pareto Criterion. (Ng, 1983).

Under certain idealized conditions, it can be shown that a system of free markets will lead to a Pareto efficient outcome. This is called the first welfare theorem. It was first demonstrated mathematically by economists Kenneth Arrow and Gerard Debreu. However, the result does not rigorously establish welfare results for real economies because of the restrictive assumptions necessary for the proof (markets exist for all possible goods, all markets are in full equilibrium, markets are perfectly competitive, transaction costs are negligible, there must be no externalities, and market participants must have perfect information). Moreover, it has since been demonstrated mathematically that, in the absence of perfect information or complete markets, outcomes will generically be Pareto inefficient (the Greenwald-Stiglitz Theorem).^[3]

Explicit consideration of Pareto-efficiency of economic factors (labor, capital) and value added of sectors is given by Dalimov (2008, 2009). It shows that a pair of the value added and labor income behave within and between regions as a linked pair obeying to the heat equation (i.e. they move as just any gas or a liquid obeying to the heat and/or diffusion equations).

Modification of the heat equation has been found as responsible for the dynamics of the factors for a case of international economic integration. Pareto-efficiency here is considered as most optimal (mathematically) re-allocation of the factors taking place due to economic integration. It fits one of clear definitons of Pareto-optimality applied to economics stating that Pareto-efficiency of economic parameters is achieved if there could be no better change of these parameters (Jovanovich, 2005). In other words, there has to be fulfilled a condition of the first spatial derivatives of the factors tending to zero after economic integration.

Economically a starting point for analysis was an idea that labor migrates to place of better wages while capital - to areas with higher returns (as example, consider unification of Germany, with labor moving from east to west, and capital being invested from West Germany to eastern part of the unified state), with direction of respective migration flows being opposite to each other. But the outcome of the analysis has shown that only value added of sectors (not capital) and annual wages of labor act as linked pair of parameters. Economically this means that businesses make value added in less developed integrated areas, while labor still moves to places with higher wages. The other straight conclusion is with the dynamic equation obtained (non-homogeneous heat equation) which for decades has been considered in physics as quite developed tool of analysis. So now one may attempt to use results previously obtained in physics and apply them for variety of tasks concerning migrating parameters in economics.

Generally, Pareto-efficiency in economics is observed when there come measures changing trade environment within considered region (either state or a group of neighbor states). This is a reason why Pareto-efficiency is one of the intrinsic features of economic integration, both theory and practice.

Formal representation

Pareto frontier

Example of a Pareto frontier. The boxed points represent feasible choices, and smaller values are preferred to larger ones. Point C is not on the Pareto Frontier because it is dominated by both point A and point B. Points A and B are not strictly dominated by any other, and hence do lie on the frontier.

Given a set of choices and a way of valuing them, the Pareto frontier or Pareto set is the set of choices that are Pareto efficient. The Pareto frontier is particularly useful in engineering: by restricting attention to the set of choices that are Pareto-efficient, a designer can make tradeoffs within this set, rather than considering the full range of every parameter.

The Pareto frontier is defined formally as follows..

Consider a design space with n real parameters, and for each design-space point there are m different criteria by which to judge that point. Let be the function which assigns, to each design-space point x, a criteria-space point f(x). This represents the way of valuing the designs. Now, it may be that some designs are infeasible; so let X be a set of feasible designs in , which must be a compact set. Then the set which represents the feasible criterion points is f(X), the image of the set X under the action of f. Call this image Y.

Now construct the Pareto frontier as a subset of Y, the feasible criterion points. It can be assumed that the preferable values of each criterion parameter are the lesser ones, thus minimizing each dimension of the criterion vector. 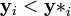Then compare criterion vectors as follows: One criterion vector y strictly dominates (or "is preferred to") a vector y* if each parameter of y is no greater than the corresponding parameter of y* and at least one parameter is strictly less: that is, for each i and for some i. This is written as to mean that y strictly dominates y*. Then the Pareto frontier is the set of points from Y that are not strictly dominated by another point in Y.

Formally, this defines a partial order on Y, namely the (opposite of the) product order on (more precisely, the induced order on Y as a subset of ), and the Pareto frontier is the set of maximal elements with respect to this order.

Algorithms for computing the Pareto frontier of a finite set of alternatives have been studied in computer science, being sometimes referred to as the maximum vector problem or the skyline query^{[4] [5]}.

Relationship to marginal rate of substitution

An important fact about the Pareto frontier in economics is that at a Pareto efficient allocation, the marginal rate of substitution is the same for all consumers. A formal statement can be derived by considering a system with m consumers and n goods, and a utility function of each consumer as z_i = fⁱ(xⁱ) where is the vector of goods, both for all i. The supply constraint is written for . To optimize this problem, the Lagrangian is used:

where λ and Γ are multipliers.

Taking the partial derivative of the Lagrangian with respect to one good, i, and then taking the partial derivative of the Lagrangian with respect to another good, j, gives the following system of equations:

for j=1,...,n. for i = 2,...,m and j=1,...,m, where f_x is the marginal utility on f' of x (the partial derivative of f with respect to x).

for i,k=1,...,m and j,s=1,...,n.

Pareto-allocation of the factors may be stated more explicitly and clearly by formulating its definition mathematically as a condition when temporal derivatives of the parameters (economic factors, such as a labor or capital) strive to zero. That means that it is indeed an optimal allocation, identical to Pareto-efficiency condition.

See also

Notes

References

• Fudenberg, D. and Tirole, J. (1983). Game Theory. MIT Press. Chapter 1, Section 2.4. 
• Ng, Yew-Kwang (1983). Welfare Economics. Macmillan. 
• Osborne, M. J. and Rubenstein, A. (1994). A Course in Game Theory. MIT Press. pp. 7. ISBN 0-262-65040-1. 
• Dalimov R.T. Modelling International Economic Integration: an Oscillation Theory Approach. Victoria, Trafford, 2008, 234 p.
• Dalimov R.T. The heat equation and the dynamics of labor and capital migration prior and after economic integration. African Journal of Marketing Management, vol. 1 (1), pp.023–031, April 2009.

Jovanovich, M. The Economics Of European Integration: Limits And Prospects. Edward Elgar, 2005, 918 p.




Retrieved from : http://en.wikipedia.org/wiki/Pareto_efficiency